3. PORCENTAJES
Un tanto por ciento o un porcentaje es una cantidad determinada de cada 100 unidades consideradas.
su simbolo es %
intervienen cuatro componentes:
Cantidad Total ---- 100 %
Cantidad Parcial ---- Porcentaje Parcial
Ejemplo
(Cantidad total) $ 1.000 - equivale al - 100 % (porcentaje total)
(Cantidad parcial) $ 500 - equivale al - 50 % (porcentaje parcial)
Existen tres situaciones o tipos de problemas que pueden plantearse. Éstos son :
1.- Dada una cantidad total, calcular el número que corresponde a ese porcentaje (%) parcial :
Ejemplo: ¿Cuál (cuanto) es el 20% de 80?
|
Cantidad
|
Porcentaje
|
Total
|
80
|
100
|
Parcial
|
x
|
20
|
Para resolverlo, se hace:
Resolvemos la incógnita (x):
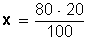
Haciendo la operación, queda:
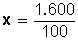
Simplificando, queda:
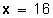
Respuesta: el 20 % de 80 es 16.
2.- Calcular el total, dada una cantidad que corresponde a un porcentaje de él.
Ejemplo: Si el 20 % de una cierta cantidad total es 120 ¿Cuál es el total?
Cantidad
|
Porcentaje
|
x
|
100
|
120
|
20
|
Para resolverlo, se hace:
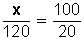
Resolvemos la incógnita (x):
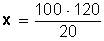
Haciendo la operación, queda:
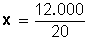
Simplificando, queda:
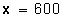
Respuesta: 120 es el 20 % de un total de 600.
3.- Dado el total y una parte de él calcular que % es esa parte del total.
Ejemplo: ¿Qué porcentaje es 40 de 120?
Cantidad
|
Porcentaje
|
120
|
100
|
40
|
x
|
Para resolverlo, se hace:
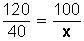
Resolvemos la incógnita (x):
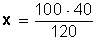
Haciendo la operación, queda:
Simplificando y haciendo la división, queda:
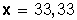
Respuesta: 40 es el 33,33 % de 120.
TAREA
http://www.calcularporcentaje.es/
http://es.calcuworld.com/calculadoras-matematicas/calculadora-de-porcentajes/
VEAMOS
EJEMPLOS DE RESOLUCIÓN DE PROBLEMAS CON PORCENTAJES :
TAREA : RESOLVER LAS PAGINAS 82 Y 83 DEL LIBRO , ACTIVIDADES 47 A 50.
