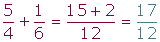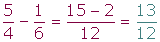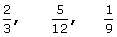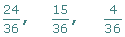POTENCIA DE NUMEROS DECIMALES

Potencia de un número decimal

Para obtener la potencia de un decimal un primer camino es realizar directamente las multiplicaciones necesarias. 

2,53=2,5·2,5·2,5=15,625

Pero si lo prefieres, también puedes operar sin decimales y añadirlos al final.

253=25·25·25=15625

El número inicial tenía 1 decimal. Su cubo tendrá 3·1=3 decimales, es decir 15,625

division de numeros decimales

División de un número decimal
Cuando el dividendo tiene decimales operaremos de la siguiente manera:

a) Primero realizaremos al división como si el dividendo fuera un número entero, sin tener en cuenta que algunas cifras son decimales.
b) Una vez resuelta la división, contaremos las cifras decimales que tiene el dividendo y serán las que lleve el cociente.

Veamos un ejemplo:

El dividendo tiene 2 cifras decimales.
En principio dividimos sin tener en cuenta esto (como si el dividendo fuera un número entero)

multiplicacion de numeros decimales

Multiplicaciones
En una multiplicación pude haber decimales en cualquiera de los dos factores, o en los dos:

a) En primer lugar multiplicamos sin tener en cuenta que hay decimales:

b) A continuación contamos los números decimales que hay en ambos factores y serán las cifras decimales que lleve el resultado:
b.1.- Empecemos por la primera multiplicación,

Tiene una cifra decimal en el primer factor y ninguna en el segundo: en total 1 cifra decimal.
El resultado de la multiplicación (324.324) llevará 1 cifra decimal:

b.2.- Segunda multiplicación,

Tiene dos cifras decimales en el segundo factor: en total 2 cifras decimales.
El resultado de la multiplicación (527.814) llevará 2 cifras decimales:

b.3.- Tercera multiplicación,

Tiene dos cifras decimales en el primer factor y una en el segundo: en total 3 cifras decimales.
El resultado de la multiplicación (255.528) llevará por tanto 3 cifras decimales:

2.- Multiplicar por 10, 100, 1.000
Por ejemplo:

45,6 x 10
235,6 x 100
78,96 x 1.000

Para calcular el resultado:

a) Primero escribimos en el resultado el primer factor.
b) Luego en el resultado desplazaremos la coma a la derecha tantas posiciones como ceros lleve el número por el que hemos multiplicado.
Puede ocurrir que haya más ceros que cifras decimales, por lo que no podamos desplazar a la derecha la coma tantas posiciones como ceros.
¿Qué hacemos? Las posiciones que no hayamos podido desplazar la coma la completaremos con ceros:

Veamos los ejemplos:
a) 45,6 x 10

Primeros repetimos en el resultado el primer factor.
45,6 x 10 = 45,6
Luego desplazaremos la coma a la derecha una posición ya que hemos multiplicado por 10 que lleva 1 cero:
45,6 x 10 = 456, (la coma a la derecha sin ninguna cifra decimal se puede quitar y escribir 456)

b) 235,6 x 100

Primeros repetimos en el resultado el primer factor.
235,6 x 100 = 235,6
Luego desplazaremos la coma a la derecha dos posiciones ya que hemos multiplicado por 100 que lleva 2 ceros:
Como 235,6 tan sólo tiene un decimal y necesitamos desplazar la coma 2 posiciones, completaremos el movimento que nos falta poniendo 1 cero:
235,6 x 100 = 23.560

c) 78,96 x 1.000

Primeros repetimos en el resultado el primer factor.
78,96 x 1.000 = 78,96
Luego desplazaremos la coma a la derecha tres posiciones ya que hemos multiplicado por 1.000 que lleva 3 ceros.
Como 78,96 tan sólo tiene dos decimales y necesitamos desplazar la coma 3 posiciones, completaremos el movimento que nos falta poniendo 1 cero:
78,96 x 1.000 = 78.960

operaciones con números decimales

ADICIÓN Y SUSTRACCION DE DECIMALES

Adición y sustracción de números decimales

Para sumar y restar números decimales debemos seguir el mismo procedimiento que utilizamos para sumar o restar números naturales, sólo que debemos alinear las comas de los sumandos, en el caso de la suma, y del minuendo y sustraendo, en el caso de la resta, y al resultado (suma o diferencia) poner la coma en la misma ubicación.
Observa los siguientes ejemplos:

Recuerda, que para números que tienen distinta cantidad de cifras decimales, podemos agregar tantos ceros como sean necesarios después de la última cifra decimal.
Así:

tarea página 71

orden de los numeros decimales

ORDEN DE LOS NUMEROS DECIMALES
al igual que anteriores unidades hemos ordendo numeros naturales , numeros enteros y numeros fraccionarios , tambien podemos ordenas numeros decimales .

procedimiento:

1. nos fijamos en su parte entera 
2. si tienen las partes enteras iguales , nos fijamos en la cifra de las décimas.
3. si tienen la cifra de las décimas iguales , nos fijamos en las cifra de las centésimas.
4. si tienen la cifra de las centésimas iguales , nos fijamos en la cifra de las milésimas y asi sucesivamente.

ejemplo:  15,82 > 14,25
                   0,3 >   0,03

Dados dos números decimales es menor:
1 El que tenga menor la parte entera.

Ejemplo:

3.528 < 5.00001 < 7.36

2 Si tienen la misma parte entera, el que tenga la menor parte decimal.

Ejemplo:

3.00001 < 3.36 < 3.528

 

 ayuda 
http://www.vitutor.com/di/d/a_3e.html

Números decimales y fracciones decimales

BLOQUE 3 

NÚMEROS DECIMALES 
VOLÚMENES DE PRISMAS Y CILINDROS

 Números decimales y fracciones decimales
los numeros decimales constan de dos partes separadas por una coma , la coma decimal.
ejemplo:

LECTURA DE NUMEROS DECIMALES

1. primero nombramos las unidades enteras
2. leemos la parte que va detras de la coma , dandole el nombre de la última unidad decimal que aparece.

ejemplo : 123,896 se lee 123 unidades 896 milesimas.

tarea  : página 69 

representacion en la recta numerica 

numero :  3, 85  ( representado por el punto rojo sobre la recta numerica)

 

fin de bloque 2

REALIZAR LAS ACTIVIDADES DE LAS 60 Y 61 HASTA MAÑANA

EVALUACIÓN DE BLOQUE 2

potenciación y radicación

POTENCIACIÓN Y RADICACIÓN

revisar cada una de las propiedades ...

tarea página 55

sucesiones con multi y divi

SUCESIONES CON MULTIPLICACIÓN Y DIVISIÓN
las sucesiones  que se forman al multiplicar un mismo número por el término anterior son conocidas como progresiones geométricas.

tarea pagina 53
ayuda

3.5 OPERACIONES COMBINADAS
En una  serie de operaciones combinadas con fracciones , se efectúan primero las operaciones indicadas entre paréntesis, después las multimplicaciones y las divisiones en el orden en que aparecen y finalmente , las adiciones y las sustracciones.

tarea pagina  52 


ayuda

3.OPERACIONES CON FRACCIONES

Suma y resta con distinto denominador

En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.
Ejemplo:

tarea: página 47 
actividades 33 a 35 


ayuda 

http://www.vitutor.com/di/r/a_6e.html


MULTIPLICAR FRACCIONES

Hay 3 simples pasos para multiplicar fracciones 1. Multiplica los números de arriba (los numeradores). 2. Multiplica los números de abajo (los denominadores). 3. Simplifica la fracción.

EJEMPLO1

1	×	2
2		5

Paso 1. Multiplica los números de arriba:

1	×	2	=	1 × 2	=	2
2		5

Paso 2. Multiplica los números de abajo:

1	×	2	=	1 × 2	=	2
2		5		2 × 5		10

Paso 3. Simplifica la fracción:

2	=	1
10		5

tarea página 48 
 
FRACCIÓN DE UNA FRACCIÓN
para calcular la fracción de una fracción :
multiplicamos ambas fracciones
ejemplo :
3 / 4  de  1 / 5  =  3 / 20

recuerda que debes simplificar las fracciones siempre que sea posible.

hasta obtener una fracción irreducible . pagina ( 44 )

tarea página 49

DIVISIÓN DE FRACCIONES 

Hay 3 simples pasos para dividir fracciones:

Paso 1. Dale la vuelta a la segunda fracción (por la que quieres dividir) (ahora es la recíproca).
Paso 2. Multiplica la primera fracción por la recíproca de la segunda. Paso 3. Simplifica la fracción (si hace falta)

Ejemplo 1

1	÷	1
2		4

Paso 1. Dale la vuelta a la segunda fracción (la recíproca):

1		4
4		1

Paso 2. Multiplica la primera fracción por la recíproca de la segunda:

1	×	4	=	1 × 4	=	4
2		1		2 × 1		2

Paso 3. Simplifica la fracción:

4	=	2
2

tarea pagina 50
 
ayuda
http://www2.gobiernodecanarias.org/educacion/17webc/eltanque/todo_mate/fracciones_e/ejercicios/division_p.html

2.3 Comparación de fracciones

para entender mejor el tema anterior :

   

 

2.2. Reduccion a minimo comun denominador

Reducción de fracciones a común denomindor .- este tema se encuentra en la página 45 del texto.
   Es el proceso por el cual se transforma dos o mas fracciones en otras equivalentes con
   el mismo denominador .
   ESTOS EJEMPLOS ESTAN ENTENDIDOS ( actividad 29 )


Ayuda 1:
proceso
Reducir varias fracciones a común denominador consiste en convertirlas en otras equivalentes que tengan el mismo denominador. Para ello:
1. Se determina el denominador común, que será el mínimo común múltiplo de los denominadores.
2. Este denominador común se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
Ejemplo:

12 = 2² · 3

9 = 3² · 3

m.c.m.(3. 12. 9) = 2² · 3² = 36 

36 / 3 = 12 * 2 =  24  respuesta numerador 1

36/ 12= 3 *5 =15  respuesta numerador 2

36/ 9 = 4 * 1 = 4  respuesta numerador 3

 fracciones buscadas :

 respuestas

  
ayuda 2.
ejercicios de repaso :
link : http://www.vitutor.com/di/r/a_4e.html

Tarea para el día miércoles : realizar los ejercicios de la actividad 30 en la pagina 45 , utilizando el     método para hallar las fracciones equivalentes con el minimo común denomindor como se indica en

la ayuda anterior .

AGENDA

HORARIO:

• LUNES: clases de recuperación 11:00 am
• MIERCOLES 
• JUEVES 
• VIERNES

BLOQUE 2: FRACCIONES EQUIVALENTES.
tema : Fracciones irreducibles
EJEMPLO:

tarea página 44
actividades : 24 a 28

UTILIZA LOS MÉTODOS DE DIVISIONES SUCESIVAS Y MÁXIMO COMÚN DIVISOR SEGÚN LO PIDA EL EJERCICIO.

PÁGINA DE REPASO :
http://www.vitutor.com/di/r/fracciones_vitutor_e.html

BIENVENIDOS A NUESTRO BLOG : OCTAVO DE BASICA "B"
Año lectivo 2014-2015





BLOQUE 2
 FRACCIÓN DE UN NÚMERO

LINK1:
 http://www.smartick.es/presentacionProblema!doEjercicioAnonimo.html?recursosDidacticosId=calcular-fracciones-de-numeros-II

Link 2:
http://www2.gobiernodecanarias.org/educacion/17webc/eltanque/todo_mate/fracnum/fracnum_p.html